die Erde als Schwarzer Strahler

Die Erde als schwarzer Strahler

Das einfachste Klimamodell führt uns direkt zurück in die Schulbänke und zwar zu den Physikstunden. Dieses Modell beschreibt, dass sich die Erdtemperatur ergibt aus der Oberflächentemperatur der Sonne und der Entfernung zwischen Erde und Sonne. Es handelt sich hierbei um eine sogenannte Strahlungsbilanz: Die Erdtemperatur ergibt sich aus der Menge der Strahlung, die die Erde von der Sonne empfängt, und der Menge, die sie selbst ins All ausstrahlt.

Elektromagnetische Strahlung

Um die Strahlungsbilanz zu verstehen, muss man wissen, dass jedes Objekt mit einer Temperatur über 0 K (K steht für Kelvin 0 K = -273,15 °C) Energie an seiner Umgebung abgibt, indem es elektromagnetische Wellen ausstrahlt (Oke, 1987). Je wärmer das Objekt ist, desto kürzer sind die Wellen der Strahlung. Abbildung 1 stellt einige dieser Bereiche dar. Die kürzesten Wellen, die dem Durchschnittsmenschen bekannt sind, sind die Röntgenstrahlung mit Wellenlängen von etwa 0,1 nm bis 10 nm (nm bedeutet Nanometer, eine Milliardeste eines Meters)(Oke, 1987). Dann kommt die UV-Strahlung mit Wellenlängen von etwa 10 nm bis 380 nm, gefolgt vom sichtbaren Licht mit Wellenlängen von etwa 380 bis 780 nm (Oke, 1987; Moene and Van Dam, 2014). Abbildung 1 zeigt, dass die Sonne die meiste Strahlung gerade in diesem Bereich ausstrahlt. Die nächste Stufe ist der sogenannte Infrarotbereich mit Wellenlängen zwischen etwa 780 nm und 1 mm (Millimeter). Dies ist der Strahlungsbereich der Erde, wobei die Erde die meiste Strahlung mit Wellenlängen von etwa 0,01 mm ausstrahlt. Darauf folgen die Mikrowellen, die wir von der Strahlung, die vom gleichnamigen Küchengerät verwendet wird, kennen. Im Mikrowellenbereich liegen die Wellenlängen zwischen 1 mm und 1 m (Oke, 1978). Schließlich gibt es noch die Radiowellen, die größer als ein Meter sind (Oke, 1987). Diese beiden letzten Bereiche sind aber in Abbildung 1 nicht mehr dargestellt.

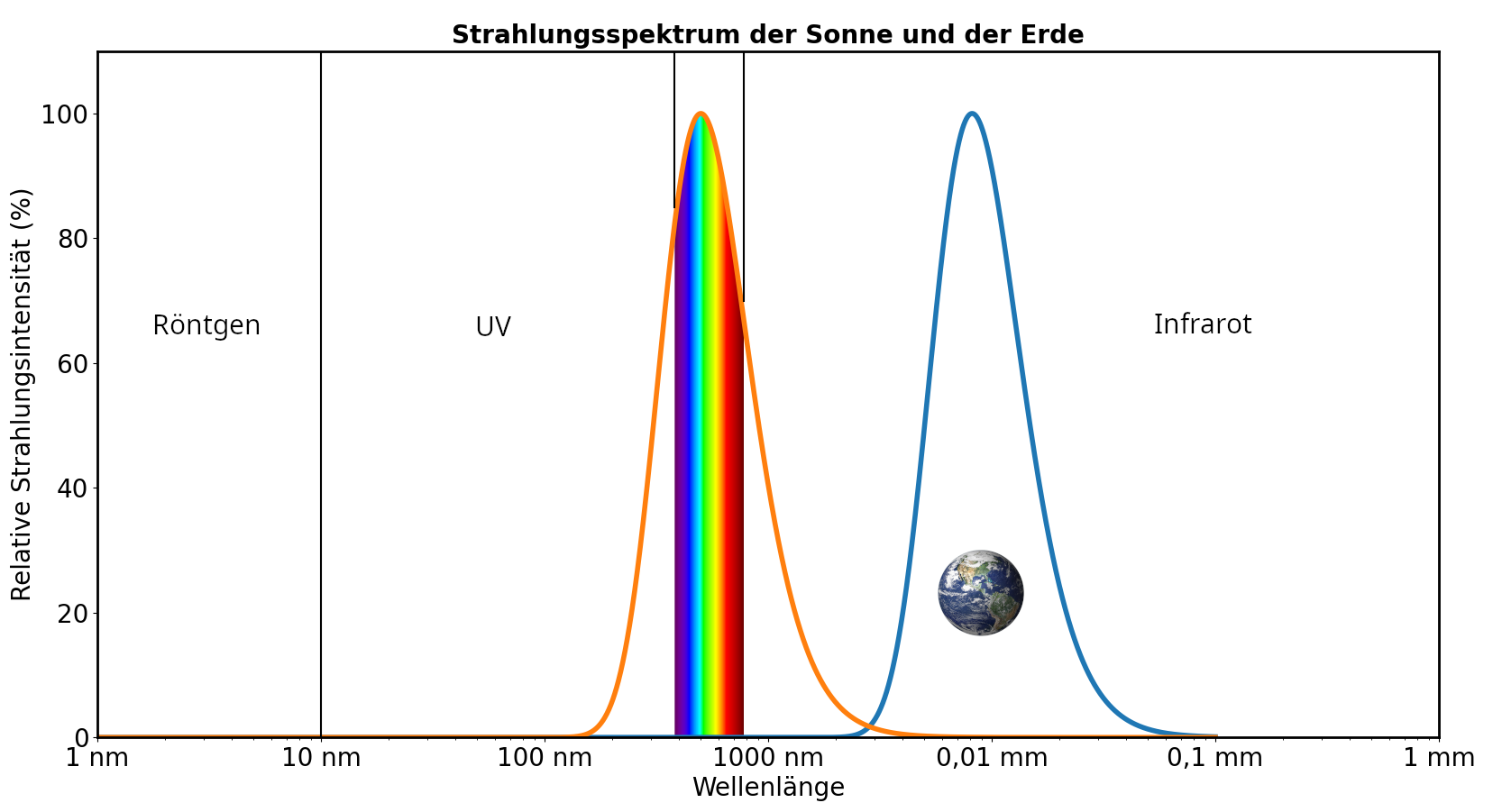
Abbildung 1 zeigt die Strahlungskurven der Sonne und der Erde normaliziert auf 100%

Abbildung 1: Strahlungskurven der Sonne und der Erde. Für die Sichtbarkeit sind die Maxima beider Kurven auf 100% normalisiert, wobei die Sonne in Wirklichkeit eine Million Mal stärker als die Erde strahlt. Die Kurven sind berechnet anhand vom Plancksches Strahlungsgesetz, Gleichung 2.13 in Stull (2017).

Mathematische Gleichungen

Um die Physik richtig anwenden zu können, benötigen wir drei einfache Formeln.

1. Die Oberfläche einer Kugel wird beschrieben durch:

O = π D^{2}

mit
O - der Oberfläche in m² (Quadratmeter)
π - der Zahl pi ≈ 3,1416
D - dem Durchmesser der Kugel in m.

2. Die Oberfläche eines Kreises wird beschrieben durch:

O = 0,25 π D^{2}

3. Die gesamte von einem Objekt ausgestrahlte Strahlung, die Strahlungsleistung, hängt mit dessen Oberfläche und Temperatur zusammen (Stull, 2017):

P = O \cdot σ {(T + 273,15)}^{4}

mit
P - der Strahlungsleistung in W (Watt)
σ - der Stefan-Boltzmann-Konstante ≈ 5,67·10^-8 W m^-2K^-4
T - der Temperatur in °C

Das Modell

Das Klimamodell beschreibt die Erdtemperatur anhand der Energiebilanz zwischen der Sonne und der Erde. Sie hängt von der Menge an Sonnestrahlung ab, die die Erde abfängt, und die Strahlung, die sie selbst ausstrahlt. Das Modell basiert auf folgenden Annahmen (Oke, 1987; Stull, 2017):

Die Sonne ist eine Kugel und strahlt perfekt in alle Richtungen aus.
Die Erde ist eine Kugel und strahlt perfekt in alle Richtungen aus.
Die Erde hat keine Atmosphäre.
Die Erde absorbiert alle Sonnenstrahlung und setzt sie in Wärme um.
Die Erde leitet ihre Wärme perfekt, sodass die Temperatur in der gesamten Erdkugel überall gleich ist.
Die Erde dreht sich in einem Kreis um die Sonne.
Die Erde reflektiert keine Sonnenstrahlung.

Zunächst möchte ich die Physik erklären, die beschreibt, wie viel Sonnenstrahlung die Erde abfängt. Abbildung 2 zeigt schematisch, wie die Sonneneinstrahlung von der Erde abgefangen wird.

Abbildung 2 zeigt wie die Sonnenstrahlung sich wie eine Kugel ins All ausbreitet und am Rande dieser Kugel von der Erde aufgefangen wird.

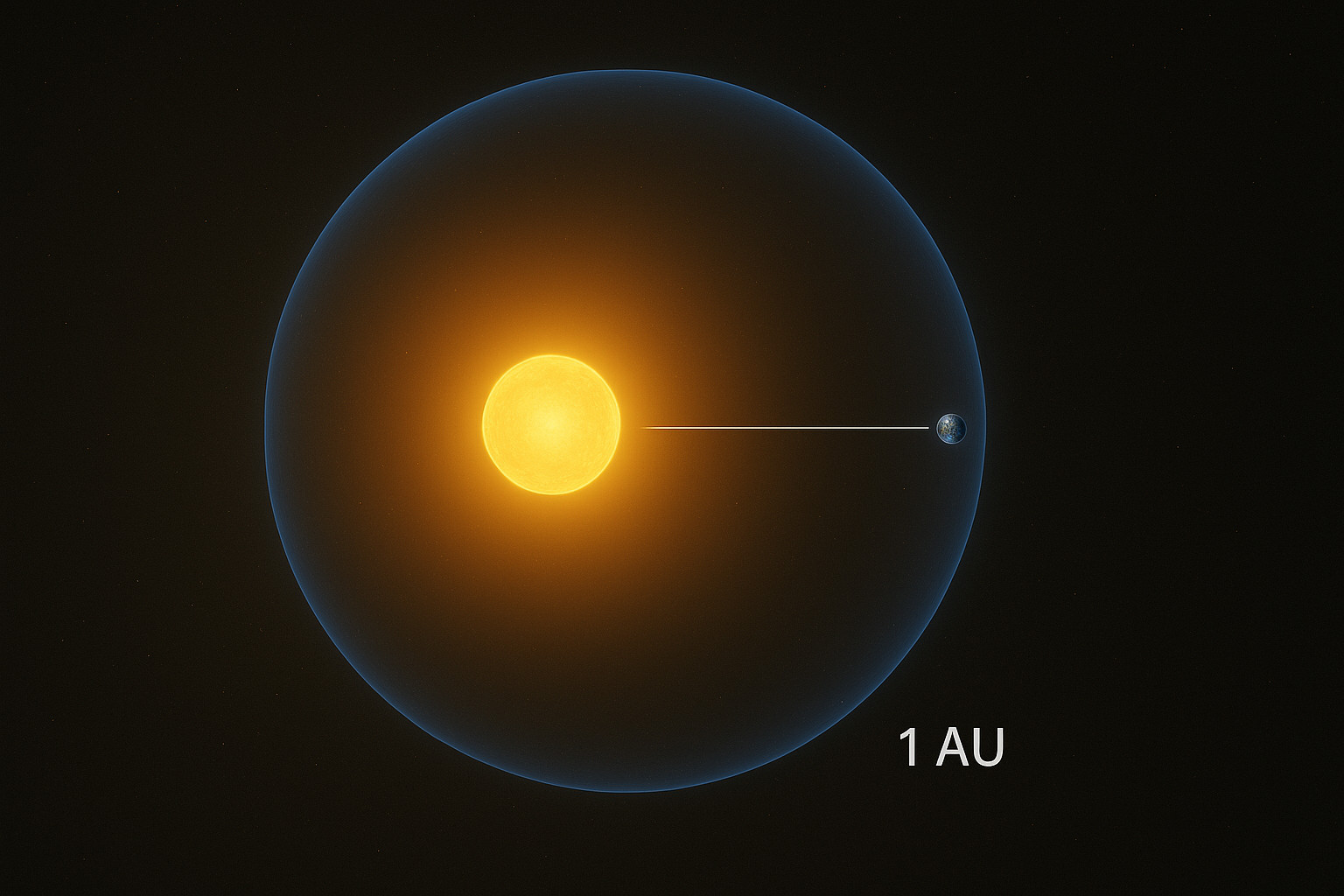
Abbildung 2: die Sonnenstrahlung verbreitet sich wie eine Kugel ins All. Ein winziger Teil wird wie in einem Kreis von der Erde, die in einer Entfernung von 1 AU (astronomical unit) steht, aufgefangen.

Die Sonnenstrahlung entsteht theoretisch im Kern der Sonne und wird dann an ihrer Oberfläche ausgestrahlt. Die gesamte Strahlungsleistung kann man schätzen, indem man die Oberfläche der Sonne (siehe Gleichung 1) berücksichtigt und dabei die Oberflächentemperatur der Sonne, T_S, sowie den Durchmesser der Sonne, D_S, in Gleichung 3 einbezieht (Stull, 2017):

P_{Sonne} = π {D_{S}}^{2} \cdot σ {(T_{S} + 273,15)}^{4}

An der Stelle, an der sich die Erde befindet, kann man sich eine zweite Kugel mit einem Durchmesser vorstellen, der die doppelten Sonne-Erde-Entfernung entspricht (siehe Abbildung 2). Das heißt, die gesamte Strahlung, die zuvor über die Sonneoberfläche verteilt wurde, wird jetzt über diese enorme Kugel mit einem Durchmesser, d, von zwei astronomischen Einheiten (2 AU) gleichmäßig verteilt. Ein winzig kleiner Teil dieser Strahlung wird von der Erde abgefangen. In dieser Entfernung ist die Erde effektiv als Kreis zu betrachten, der das Licht blockiert. Das heißt, würde man eine Wand hinter die Erde aufstellen, dann wäre ein kreisförmiger Schatten mit folgender Oberfläche (siehe Gleichung 2) sichtbar (Stull, 2017):

O_{Erdschatten} = 0,25 π {D_{E}}^{2}

wobei D_E der Durchmesser der Erde ist. Um die gesamte, von der Erde abgefangene Strahlung, S_in, zu berechnen, muss zunächst die Strahlungsintensität abgeschätzt werden. Diese Strahlungsintensität wird gemeinhin als Solarkonstante bezeichnet und entspricht der Sonnestrahlung pro Quadratmeter in der Entfernung, in der sich die Erde von der Sonne befindet (Stull, 2017). Dazu teilt man die gesamte Sonnestrahlung, P_Sonne, durch die Oberfläche dieser riesigen Kugel, $π d^{2}$ . Da der Erdschatten nicht nur einen Quadratmeter groß ist, muss dieser Wert noch mit der Oberfläche des Erdschattens multipliziert werden, um die gesamte Strahlung zu bekommen. In Gleichungsform ist das (Stull, 2017):

S_{in} = \frac{P_{Sonne}}{π d^{2}} \cdot O_{Erdschatten} = \frac{π {D_{S}}^{2} \cdot σ {(T_{S} + 273,15)}^{4}}{π d^{2}} \cdot 0,25 π {D_{E}}^{2}

Die Energie, die die Erde ausstrahlt, ist einfacher zu berechnen. Dies erfolgt anhand von Gleichungen 1 und 3 unter Verwendung des Erddurchmessers, D_E und deren Temperatur, T_E, die wir ermitteln möchten. In Gleichungsform ergibt sich (Stull, 2017):

S_{aus} = π {D_{E}}^{2} \cdot σ {(T_{E} + 273,15)}^{4}

Die Gleichgewichtstemperatur

Das Modell besagt, dass die Erde genau so viel Strahlung ausstrahlt, wie sie empfängt, sodass wir sagen können S_in = S_aus. Macht man die Mathematik und streicht einige Parameter gegeneinander weg, dann ergibt sich folgende Gleichung (Stull, 2017):

T_{E} = {0,25}^{\frac{1}{4}} \cdot (T_{S} + 273,15) {(\frac{D_{S}}{d})}^{\frac{1}{2}} - 273,15

mit
T_E - der Erdtemperatur in °C
T_S - der Temperatur der Sonne in °C (= 5498,85 °C)
D_S - dem Durchmesser der Sonne in m (≈ 1.3914·10⁹ m)
d - dem doppelten Abstand zwischen Sonne und Erde in m (2 AU ≈ 2,992·10¹¹ m) (Williams, 2025)

Wenn wir mit dieser Gleichung die Erdtemperatur berechnen, ergibt sich ein Wert von 5,2 °C. Zum Vergleich: Für den Mars, der mit 228 Millionen Kilometern etwa 1,5-mal so weit von der Sonne entfernt ist, würde die Temperatur -47,7 °C betragen. Für die Venus, die mit 108 Millionen Kilometern etwa 1,4-mal näher an der Sonne steht, würde die Temperatur dagegegen 54,1 °C betragen (Entfernungswerte von Williams (2025)). Das Modell besagt also, dass ein Planet umso kälter ist, je weiter er von der Sonne entfernt ist. Die Größe des Planeten spielt dabei keine Rolle.

Auf der nächsten Seite, werden wir uns mit der Albedo beschäftigen. Klicken Sie hier, um weiter zu lesen.

Quellen und Literatur:
* Moene AF and Van Dam JC (2014) Transport in the atmosphere–vegetation–soil continuum. New York: Cambridge university press. 446 pages. ISBN 978-0-521-19568-3, https://doi.org/10.1017/CBO9781139043137
* Oke TR (1987) Boundary Layer Climates; Methuen; Psychology Press: New York, NY, USA, 435 pages, ISBN 0-415-04319-0
* Stull R (2017) Practical Meteorology: An Algebra-based Survey of Atmospheric Science -version 1.02b. Univ. of British Columbia. 940 pages. ISBN 978-0-88865-283-6 (https://www.eoas.ubc.ca/books/Practical_Meteorology/index.html).
* Williams DR (2025) NASA Planetary Factsheet, https://nssdc.gsfc.nasa.gov/planetary/factsheet/

Klimasystem